domingo, 5 de agosto de 2012
La Estadística inferencial o Inferencia estadística estudia cómo sacar conclusiones generales para toda la población a partir del estudio de una muestra, y el grado de fiabilidad o significación de los resultados obtenidos.
Muestreo probabilístico
Consiste en elegir una muestra de una población al azar. Podemos distinguir varios tipos de muestreo:
Muestreo aleatorio simple
Para obtener una muestra, se numeran los elementos de la población y se seleccionan al azar los n elementos que contiene la muestra.
Muestreo aleatorio sistemático
Se elige un individuo al azar y a partir de él, a intervalos constantes, se eligen los demás hasta completar la muestra.
Por ejemplo si tenemos una población formada por 100 elementos y queremos extraer una muestra de 25 elementos, en primer lugar debemos establecer el intervalo de selección que será igual a 100/25 = 4. A continuación elegimos el elemento de arranque, tomando aleatoriamente un número entre el 1 y el 4, y a partir de él obtenemos los restantes elementos de la muestra.
2, 6, 10, 14,..., 98
Muestreo aleatorio estratificado
Se divide la población en clases o estratos y se escoge, aleatoriamente, un número de individuos de cada estrato proporcional al número de componentes de cada estrato.
En una fábrica que consta de 600 trabajadores queremos tomar una muestra de 20. Sabemos que hay 200 trabajadores en la sección A, 150 en la B, 150 en la C y 100 en la D.
Un muestreo puede hacerse con o sin reposición, y la población de partida puede ser infinita o finita.
En todo nuestro estudio vamos a limitarnos a una población de partida infinita o a muestreo con reposición.
Si consideremos todas las posibles muestras de tamaño n en una población, para cada muestra podemos calcular un estadístico (media, desviación típica, proporción, ...) que variará de una a otra.
Así obtenemos una distribución del estadístico que se llama distribución muestral.
Teorema central del límite
Si una población tiene media μ y desviación típica σ, y tomamos muestras de tamaño n (n>30, ó cualquier tamaño si la población es "normal"), las medias de estas muestras siguen aproximadamente la distribución:
Estimación de parámetros
Es el procedimiento utilizado para conocer las características de un parámetro poblacional, a partir del conocimiento de la muestra.
Con una muestra aleatoria, de tamaño n, podemos efectuar una estimación de un valor de un parámetro de la población; pero también necesitamos precisar un:
Intervalo de confianza
Se llama así a un intervalo en el que sabemos que está un parámetro, con un nivel de confianza específico.
Nivel de confianza
Probabilidad de que el parámetro a estimar se encuentre en el intervalo de confianza.
El nivel de confianza (p) se designa mediante 1 − α.
Error de estimación admisible
Que estará relacionado con el radio del intervalo de confianza.
Estimación de la media de una población
El intervalo de confianza, para la media de una población, con un nivel de confianza de 1 − α , siendo x la media de una muestra de tamaño n y σ la desviación típica de la población, es:
El error máximo de estimación es:
Cuanto mayor sea el tamaño de la muestra, n, menor es el error.
Cuanto mayor sea el nivel de confianza, 1-α, mayor es el error.
Tamaño de la muestra
Si aumentamos el nivel de confianza, aumenta el tamaño de la muestra.
Si disminuimos el error, tenemos que aumentar el tamaño de la muestra.
El tiempo que tardan las cajeras de un supermercado en cobrar a los clientes sigue una ley normal con media desconocida y desviación típica 0,5 minutos. Para una muestra aleatoria de 25 clientes se obtuvo un tiempo medio de 5,2 minutos.
1.Calcula el intervalo de confianza al nivel del 95% para el tiempo medio que se tarda en cobrar a los clientes.
2.Indica el tamaño muestral necesario para estimar dicho tiempo medio con un el error de ± 0,5 minutos y un nivel de confianza del 95%.
n ≥ 4
Estimación de una proporción
Si en una población, una determinada característica se presenta en una proporción p, la proporción p' , de individuos con dicha característica en las muestras de tamaño n, se distribuirán según:
Intervalo de confianza para una proporción
El error máximo de estimación es:
En una fábrica de componentes electrónicos, la proporción de componentes finales defectuosos era del 20%. Tras una serie de operaciones e inversiones destinadas a mejorar el rendimiento se analizó una muestra aleatoria de 500 componentes, encontrándose que 90 de ellos eran defectuosos. ¿Qué nivel de confianza debe adoptarse para aceptar que el rendimiento no ha sufrido variaciones?
p = 0.2 q = 1 - p =0.8 p'= 90/ 500 = 0.18
E = 0.2 - 0.18 = 0.02
P (1 - zα/2 <1.12) = 0.86861 - 0.8686 = 0.1314
0.8686 - 0.1314 = 0.737
Nivel de confianza: 73.72%
Contraste de hipótesis
Hipótesis estadísticas
Un test estadístico es un procedimiento para, a partir de una muestra aleatoria y significativa, extraer conclusiones que permitan aceptar o rechazar una hipótesispreviamente emitida sobre el valor de un parámetro desconocido de una población.
La hipótesis emitida se designa por H0 y se llama hipótesis nula.
La hipótesis contraria se designa por H1 y se llama hipótesis alternativa.
Contrastes de hipótesis
1. Enunciar la hipótesis nula H0 y la alternativa H1.
Bilateral
H0=k
H1 ≠ k
Unilateral
H0≥ k
H1 < k
H0 ≤k
H1> k
2. A partir de un nivel de confianza 1 − α o el de significación α. Determinar:
El valor zα/2 (bilaterales), o bien zα (unilaterales)
La zona de aceptación del parámetro muestral (x o p').
3. Calcular: x o p', a partir de la muestra.
4. Si el valor del parámetro muestral está dentro de la zona de la aceptación, se acepta la hipótesis con un nivel de significación α. Si no, se rechaza.
Contraste bilateral
Se presenta cuando la hipótesis nula es del tipo H0: μ = k (o bien H0: p = k) y la hipótesis alternativa, por tanto, es del tipo H1: μ≠ k (o bien H1: p≠ k).
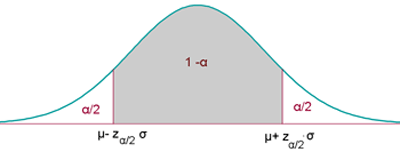
El nivel de significación α se concentra en dos partes (o colas) simétricas respecto de la media.
La región de aceptación en este caso no es más que el correspondiente intervalo de probabilidad para x o p', es decir:
o bien:
Se sabe que la desviación típica de las notas de cierto examen de Matemáticas es 2,4. Para una muestra de 36 estudiantes se obtuvo una nota media de 5,6. ¿Sirven estos datos para confirmar la hipótesis de que la nota media del examen fue de 6, con un nivel de confianza del 95%?
1. Enunciamos las hipótesis nula y alternativa:
H0 : μ = 6 La nota media no ha variado.
H1 : μ ≠ 6 La nota media ha variado.
2. Zona de aceptación
Para α = 0.05, le corresponde un valor crítico: zα/2 = 1.96.
Determinamos el intervalo de confianza para la media:
(6-1,96 · 0,4 ; 6+1,96 · 0,4) = (5,22 ; 6,78)
3. Verificación.
Valor obtenido de la media de la muestra: 5,6 .
4. Decisión
Aceptamos la hipótesis nula H0, con un nivel de significación del 5%.
Contraste unilateral
Caso 1
La hipótesis nula es del tipo H0: μ ≥ k (o bien H0: p ≥ k).
La hipótesis alternativa, por tanto, es del tipo H1: μ < k (o bien H1: p < k).
Valores críticos
1 − α
α
z α
0.90
0.10
1.28
0.95
0.05
1.645
0.99
0.01
2.33
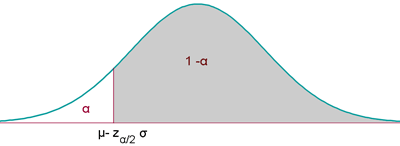
El nivel de significación α se concentra en una parte o cola.
La región de aceptación en este caso será:
o bien:
Un sociólogo ha pronosticado, que en una determinada ciudad, el nivel de abstención en las próximas elecciones será del 40% como mínimo. Se elige al azar una muestra aleatoria de 200 individuos, con derecho a voto, 75 de los cuales estarían dispuestos a votar. Determinar con un nivel de significación del 1%, si se puede admitir el pronóstico.
1. Enunciamos las hipótesis nula y alternativa:
H0 : μ ≥ 0.40 La abstención será como mínimo del 40%.
H1 : μ < 0.40 La abstención será como máximo del 40%;
2. Zona de aceptación
Para α = 0.01, le corresponde un valor crítico: zα = 2.33.
Determinamos el intervalo de confianza para la media:
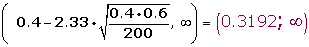
3.Verificación.
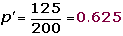
4.Decisión
Aceptamos la hipótesis nula H0. Podemos afirmar, con un nivel de significación del 1%, que la La abstención será como mínimo del 40%.
Caso 2
La hipótesis nula es del tipo H0: μ ≤ k (o bien H0: p ≤ k).
La hipótesis alternativa, por tanto, es del tipo H1: μ > k (o bien H1: p > k).
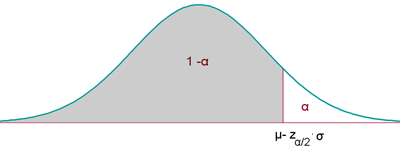
El nivel de significación α se concentra en la otra parte o cola.
La región de aceptación en este caso será:
o bien:
Un informe indica que el precio medio del billete de avión entre Canarias y Madrid es, como máximo, de 120 € con una desviación típica de 40 €. Se toma una muestra de 100 viajeros y se obtiene que la media de los precios de sus billetes es de 128 €.
¿Se puede aceptar, con un nivel de significación igual a 0,1, la afirmación de partida?
1. Enunciamos las hipótesis nula y alternativa:
H0 : μ ≤ 120
H1 : μ > 120
2.Zona de aceptación
Para α = 0.1, le corresponde un valor crítico: zα = 1.28 .
Determinamos el intervalo de confianza:
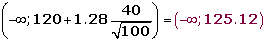
3. Verificación.
Valor obtenido de la media de la muestra: 128 € .
4. Decisión
No aceptamos la hipótesis nula H0. Con un nivel de significación del 10%.
Errores de tipo I y tipo II
Error de tipo I. Se comete cuando la hipótesis nula es verdadera y, como consecuencia del contraste, se rechaza.
Error de tipo II. Se comete cuando la hipótesis nula es falsa y, como consecuencia del contraste se acepta.
H0
Verdadera
Falsa
Aceptar
Decisón correcta
Probabilidad = 1 − α
Decisión incorrecta:
ERROR DE TIPO II
Rechazar
ERROR DE TIPO I
Probabilidad = α
Decisión correcta
La probabilidad de cometer Error de tipo I es el nivel de significación α.
La probabilidad de cometer Error de tipo II depende del verdadero valor del parámetro. Se hace tanto menor cuanto mayor sea n.
sábado, 4 de agosto de 2012
PRUEVAS ESTADISTICOS
Una investigación bien planificada debe incluir en su diseño referencias precisas acerca de las técnicas estadísticas que se utilizan en el análisis de los datos.
El análisis estadístico es el procedimiento objetivo por medio del cual se puede aceptar o rechazar un conjunto de datos como confirmatorios de una hipótesis, conocido el riesgo que se corre -en función de la probabilidad- al tomar tal decisión. En las últimas décadas, el desarrollo de las pruebas estadísticas se ha incrementado a tal grado que en la actualidad se cuenta con varias pruebas alternativas, las cuales se pueden usar para casi todo diseño experimental, de modo que el investigador se encuentra ante el dilema de seleccionar la más apropiada y económica, para las preguntas que, mediante la investigación, desea contestar.
Ante esa situación, es necesario tener una base racional, por medio de la cual se seleccione la prueba más apropiada. Esta selección constituye el punto crítico del análisis estadístico.
En la selección de una prueba estadística, se deben aplicar los criterios siguientes:
- Tipo de escala.
- Hipótesis.
- Potencia y eficiencia de la prueba.
- Características muestrales.
- Tendencia rectilínea o curvilínea del fenómeno.
Tipo de escala
En las observaciones de una investigación se puede dar una medición que en este campo consiste en asignar números a objetos y eventos de acuerdo con reglas de la lógica aceptables.
El sistema numérico es una creación altamente lógica, que ofrece múltiples posibilidades, para manifestaciones también de carácter lógico. Si se puede, de manera legítima, asignar números al describir características, objetos y eventos, será factible operar con ellos en todos sus modos permisibles y, de esas operaciones, derivar conclusiones aplicables a los fenómenos observados y medidos. Entonces, se justifica describir cosas reales por medio de números, siempre y cuando exista un grado de isomorfismo (semejanza de propiedades) entre las cosas reales y el sistema numérico, es decir, ciertas propiedades de los números deben tener paralelismo con los fenómenos observados, para que confiadamente se pueda asignar los números.
Tres propiedades fundamentales de los números permiten su aplicación en el campo de la investigación científica: identidad, ordinalidad y aditividad.
- IdentidadGrupo de 200 niños con y sin estrabismo.
Cada número sólo es igual a sí mismo, de manera que ningún otro es igual a él, es decir, posee identidad y, por lo tanto, a cualquier objeto o evento diferenciable de los demás, que tenga identidad, se le podrá aplicar un número. Este carácter de identidad de los números de origen a la escala nominal, que es un método para identificar cualitativamente los distintos objetos y eventos, y resulta obvio que no se le puede dar ningún significado cuantitativo, por ejemplo: si en un modelo experimental se cuenta una serie de clases, en las cuales se consignan sus frecuencias, éstas revelan un conjunto de cada clase.
Bajo el contexto de la tabla anterior, una muestra de 200 individuos en edad infantil se ha clasificado en dos grupos por sexo (masculino y femenino) y por la presencia o ausencia de estrabismo. Como punto de partida, la operación de escalamiento consiste en que, a partir de una clase dada, se forman subclases que se excluyen mutuamente. La única relación implicada es la de equivalencia, esto es, los miembros de cualquier subclase deben ser equivalentes en la propiedad de medida. A su vez, la relación de equivalencia es reflexiva, simétrica y transitiva.Por otro lado, las frecuencias informan de conjuntos de niños o serie de clases con una categoría e identidad, que dan una medida de las observaciones y son los valores sujetos a operaciones aritméticas. En estas condiciones, se puede contrastar hipótesis de la distribución de los casos, mediante la aplicación de pruebas estadísticas no paramétricas del tipo de prueba binomial, ji cuadrada y McNemar. Todas estas pruebas son apropiadas para datos nominales, pues revelan las frecuencias en las categorías, es decir, en datos enumerativos. - Ordinalidad
Además de contar con la propiedad de identidad, las pruebas también tienen un orden o rango siempre mayor que otro, el cual le precede en un continuum ascendente. Los objetos y eventos susceptibles de un ordenamiento a lo largo de un continuum tienen una escala ordinal.Las escalas ordinales se emplean frecuentemente en la investigación clínica, en la que el refinamiento cuantitativo a veces no es posible; por ejemplo: cuando se clasifica una respuesta en pacientes bajo los términos sin cambio, mejorado, curado, esto indica un rango de orden y clasificación.En conclusión, cabe establecer que mientras las escalas nominales sólo clasifican, las ordinales clasifican y ordenan, de manera que dan como resultado una serie de clases y categorías mutuamente exclusivas, llamadas rangos. - Aditividad
Es importante comprender que los números tienen propiedad aditiva, lo cual quiere decir que la suma de un número con otro debe dar un tercer número único. Esta propiedad de los números no sólo identifica y ordena, sino además puede sujetarse a todas las operaciones aritméticas de los números. Las conclusiones de tales operaciones son válidas para las observaciones y dan lugar a la denominada escala de intervalo.De las mediciones que en el terreno de la investigación se hayan realizado, puede inferirse que el tipo de escala (nominal, ordinal e intervalo), de modo que éste es el primer paso para elegir un procedimiento estadístico: la prueba paramétrica y la no paramétrica.Mediciones, variables y escala para la elección de la prueba estadística.
Hipótesis
La declaración de la hipótesis alterna (Ha) que se desea analizar debe ser precisa, tan completa como resulte posible, pues se trata de la aseveración operacional de la hipótesis de investigación por el experimentador. Debe precisar la dirección que se espera o la ausencia de dirección. Este último punto es fundamental para decidir si la prueba estadística por elegir será de una o dos colas.
Conjuntamente al proceso anterior, se declara la hipótesis nula (Ho), en la cual simplemente se establece la ausencia de diferencia y se declara, pare percibir con claridad, que la hipótesis se ajusta a la prueba estadística. Esto significa que al analizar un conjunto de observaciones, éstas deben sujetarse a un ensayo de hipótesis nula, condición en la que se basan todas las pruebas estadísticas.
El investigador, al contrastar hipótesis de diferencias y/o correlación, lo establece en función de una hipótesis alterna (Ha) -punto fundamental de la experimentación-, en contra de la hipótesis nula (Ho). Para decidirse por una o por la otra, debe proponerse un razonable nivel de significancia, desde antes de aplicar la prueba estadística.
El nivel de significancia o significación corresponde al límite de confianza, del riesgo de error, que enjuicia el investigador para aceptar su Ha como verdadera. De manera universal y arbitraria, dicho nivel se ha fijado en 0.05 y 0.01 de error y en 0.95 y 0.99 de certeza para aceptar hipótesis en el área psicológica, por que se espera un 5% de variación en las mediciones.
En la teoría contemporánea de la decisión estadística, se han tratado de rechazar los procedimientos que implican adhesión al nivel de significancia comentados, y se favorece el uso de procedimientos en los que las decisiones se toman en términos de función de pérdida, utilizando principios de minimax; sin embargo, aunque parece conveniente esta técnica, las posibilidades de aplicación práctica son dudosas en gran parte, en la investigación psicológica.
Contrariamente a lo anterior, también se debe establecer la zona de rechazo, la cual corresponde al límite de confianza, en que el investigador rechaza la hipótesis alterna y acepta la hipótesis nula.
Bajo los términos expresados, el investigador debe ser meticuloso al elegir la prueba estadística y al plantear la hipótesis, el nivel de significancia y la zona de rechazo, en virtud de que es factible cometer dos errores graves en la decisión estadística:
- Error del tipo I. Rechazar la hipótesis nula (Ho), siendo verdadera.
- Error del tipo II. Aceptar la hipótesis nula (Ho), siendo falsa.
Debe quedar claro que en cualquier inferencia estadística existe el peligro de cometer cualquiera de los errores mencionados y que el investigador equilibre en un nivel óptimo las propiedades de incurrir en uno u otro tipo de error.
La probabilidad de cometer un error del tipo I está dada por a (alfa), de manera que cuanto mayor sea alfa, más probable será que Ho se rechace, siendo verdadera; a su vez, el error de tipo II está representado por b (beta). La siguiente figura muestra una escala de falso a verdadero, donde cero es falso y el valor uno verdadero.
| Escala de probabilidad. |
Entre el 0 y el 1 existen valores intermedios, mientras que donde marca 0.95 existe una diferencia de 0.05 con respecto a 1. Este límite corresponde al nivel de significancia o error alfa, donde todo valor igual o meno que 0.05 se acepta Ha. Por lo tanto, 1 - alfa = beta. Se dice que en esta circunstancia, el investigador elige una cola en la decisión estadística. Por otra parte, cuando además de imponer un valor de alfa razonablemente pequeño para aceptar Ha, también define un valor de beta para aceptar Ho, elige dos colas.
De no decidir entre una u otra hipótesis, el investigador se plantea la alternativa de aumentar el tamaño de la muestra, para que el fenómeno se define con más claridad y la decisión en el contraste de la hipótesis sea más consistente.
|
Eficiencia de la prueba
La validez del análisis estadístico depende mucho de la eficacia de la prueba estadística empleada. Se acepta que una prueba estadística es eficaz cuando tiene una probabilidad muy pequeña de rechazar una hipótesis verdadera, y una alta probabilidad de rechazar la hipótesis cuando ésta es falsa. En presencia de dos pruebas estadísticas, cuya probabilidad de rechazar hipótesis falsas sea igual, la selección en principio debe inclinarse hacia la prueba que tenga la mayor probabilidad de aceptar la hipótesis cuando es verdadera.
La pruebas estadísticas se dividen en dos grandes grupos: paramétricas y no paramétricas. Las primeras son aquellas cuyo modelo especifica ciertas condiciones o premisas que debe tener la población, de la cual se ha derivado la muestra bajo análisis; además se requiere expresar las observaciones en escala de intervalo o tasa. Por otra parte, las pruebas no paramétricas, como su nombre lo indica, no requieren satisfacer esas condiciones o premisas.
Las pruebas paramétricas son las más eficaces y de uso común en la investigación, como las de comparación de promedios o prueba t de Student y la de análisis de varianza de Fischer. Ambos procedimientos deben cumplir las premisas siguientes:
- Las observaciones deben ser independientes. Al seleccionar un caso, para incluirlo en la muestra, no se deben prejuiciar las probabilidades de selección de ningún otro caso de la población, asimismo, la puntuación que se dé a una observación no debe prejuiciar a ninguna otra.
- Las poblaciones deben provenir de universos cuya distribución siga una curva normal.
- Las poblaciones deben tener la misma varianza, aunque en casos especiales es suficiente con saber la tasa de sus varianzas.
- Las variables consideradas en el estudio deben ser medidas por lo menos en escala de intervalo, para que sea posible hacer operaciones aritméticas.
Cuando por cualquier razón no se puedan cumplir los requisitos de las pruebas paramétricas, el investigador podrá recurrir a las llamadas pruebas alternas, como la prueba t de Student-Welch, la F asimilada de Cochran y la F de Tukey. En ellas no hay exigencia de homogeneidad de varianzas y, auxiliadas por un modelo matemático de ajuste, se puede obtener una eficacia que es muy cercana a la de las pruebas t de Student y de análisis de varianza.
Cabe señalar que, conforme menos condiciones o presunciones exige una prueba estadística, en que se basa su modelo matemático, más generales son sus conclusiones derivadas de su aplicación; sin embargo, también es menos eficaz para rechazar la influencia del azar, cuando éste no desempeña un papel importante.
Cuando las observaciones en escala de intervalo no se ajustan a las premisas de las pruebas paramétricas, el investigador debe estimar la pérdida de eficacia para decidir utilizar los procedimientos no paramétricos, y transformar aquellas en escalas nominales u ordinales.
Características muestrales
La manera en que influye la muestra para elegir una prueba estadística está en función de su tamaño, selección y distribución en el diseño experimental.
- Tamaño de la muestra
Anteriormente se habló de que la eficacia de una prueba estadística disminuye cuando se reducen las condiciones o premisas del modelo; sin embargo, a medida que aumenta el tamaño de la muestra, se incrementa también la eficacia.
Dicha aseveración generalmente es verdadera para muestras de tamaño definido, pero pueden carecer de veracidad al compararse dos pruebas estadísticas con muestras de tamaños diferentes, es decir, si con un tamaño de 30 por cada grupo, una prueba A puede ser más eficaz que la prueba B; en cambio, la prueba B es más eficaz que A cuando ésta sólo cuenta con un tamaño de muestra igual a 20. En otras palabras, se puede evitar escoger entre potencias y generalización, para lo cual se selecciona una prueba estadística que tenga amplia generalización, y luego aumentar su eficacia, comparable a la prueba más útil, incrementando el tamaño de la muestra. - Selección de la muestra
Las muestras por analizar pueden ser independientes y dependientes o relacionadas.- Muestras independientes. Son aquellas cuyo universo de población resulta diferente, lo cual no quiere decir que provengan de áreas desconocidas, sino que, en términos de estadística, la fenomenología estudiada puede ser consecuencia de variables distintas y que, por cada variable existente, hay un universo finito o infinito; por ejemplo, en la Tierra hay un número finito de seres humanos, pero la variable sexo divide en dos universos diferentes: hombres y mujeres. En el mismo sentido, el estado civil define otros universos distintos, solteros, casados, divorciados, viudos, etc. De esta manera, se pueden enumerar múltiples variables, que dan lugar a una infinidad de universos muestrales, de donde es factible elegir muestras independientes.
- Muestras dependientes o relacionadas. Se refieren a las provenientes de un universo muestral, a las que se aplicará un plan experimental, mediante el cual se espera un cambio, que obligadamente exige un punto de referencia de no cambio. Para esta condición, el mismo grupo experimental sirve como control o testigo, en el momento previo al tratamiento. De esta manera, en el análisis de las observaciones existen dos períodos: antes y después del tratamiento.
- Distribución de la muestra en el diseño experimental
En los diseños experimentales, el número de muestras con que está elaborado el modelo de investigación tiene singular valor para elegir la prueba estadística, pues las conclusiones a que se llegue al no aplicar la prueba adecuada darán lugar a falsas interpretaciones del experimento.En los modelos de investigación, se puede contar con una, dos o muchas muestras. Asimismo, puede tratarse de muestras independientes o dependientes o relacionadas. Estas características dan un atributo al diseño experimental, que obliga a analizar los datos de manera diferente, acorde con el modelo estadístico que mejor se ajuste a contestar las preguntas planteadas por la hipótesis. Para saber si los pacientes han alcanzado una total remisión de la enfermedad, se atiende a los hallazgos de tiempo de sobrevida y a las alteraciones clínicas de la patología. Si cuenta con varios tratamientos, se plantea la pregunta de cuál de ellos ha sido más efectivo. Así, se puede decir que una investigación cuanta con subclases diferentes. Para analizar sus observaciones y tomar una decisión de la efectividad de los tratamientos, se pueden elegir las pruebas estadísticas diseñadas para contrastar una hipótesis y para una muestra.Un ejemplo válido es el de un investigador que trabaja con roedores, para estudiar las características conductuales de agresividad y la concentración de neurotrasmisores en el sistema nervioso central. El conjunto de la muestra está constituido por cobayos, ratas y ratones, que representan grupos con tres gradientes de agresividad. En estas condiciones, el diseño experimental tiene tres muestras independientes. La elección de la prueba estadística se basará en las dos características y en el tipo de escala de las mediciones. En el supuesto de que las concentraciones de neurotrasmisores tenga una medición cuantitativa, una variable continua, una escala de intervalo y una distribución normal, con varianzas homogéneas, la elección más adecuada será el análisis de varianzas de Fischer de una entrada. Si la decisión del investigador fuera utilizar la prueba t de Student, diseñada para dos muestras, cometería tres errores graves: a) pérdida de tiempo, b) las comparaciones serían múltiples, tantas como combinaciones existan (cobayos con ratas, cobayos con ratones y ratas con ratones), c) el más trascendente, desde el punto de vista de la decisión estadística: las conclusiones a que se llegue no serán consecuencia de comparaciones independientes, sino resultarán aisladas y en pequeños pares de grupos de contraste. Es decir, si el investigador supone de antemano que entre los grupos existe variación en el grado de agresividad, perderá la información que la variación entre y dentro de grupos le demuestre la existencia de una diferencia verdadera, al no incluir simultáneamente a los tres grupos.El ejemplo descrito permite comprender que cuando se analizan simultáneamente diversos grupos de muestras, las variaciones manifestadas entre los grupos de estudio dan lugar a una diferenciación falsa o verdadera. Los contrastes parciales que se verifiquen llevan el título de independientes, porque se supone una simultánea variación o discordancia entre los grupos. Así, se dice que, en estas condiciones, el modelo experimental conserva ortogonalidad.A veces, debido al diseño creado por el investigador, se proponen comparaciones con un modelo de referencia, en el cual se supone la no existencia de modificaciones con respecto a la aplicación de tratamientos o variables. Estos grupos, también denominados control o testigo, servirán de línea base para medir los cambios que pudieran presentarse en los otros grupos. De esta manera, la magnitud del cambio será dependiente de lo que suceda en el control. Este tipo de diseño experimental, debido a las comparaciones dependientes, ha perdido ortogonalidad. (Con mediciones de intervalo, se tiene la prueba de Tukey.)
Tendencia rectilínea o curvilínea del fenómeno
Cuando la hipótesis resulta probar la asociación o correlación de variables, es importante conocer la linealidad del fenómeno. Si es rectilíneo y tiene una escala de intervalo, la aplicación del coeficiente de correlación de Pearson parece adecuada; pero si este mismo procedimiento se aplica a un fenómeno curvilíneo -aún cuando exista una verdadera asociación-, dará lugar a aceptar hipótesis de no asociación.
Un fenómeno curvilíneo puede tornarse en rectilíneo, mediante transformaciones matemáticas (logaritmos, función recíproca, seno, coseno, etc.) y así aplicar la correlación de Pearson.
Si se desconoce la linealidad, se deberá utilizar la prueba de análisis de covarianza para determinar la función matemática más acorde con el fenómeno estudiado.
Suscribirse a:
Entradas (Atom)